最高のコレクション •Žq ‚Ì ƒoƒXƒP ƒ‰ƒXƒg ƒQ[ƒ€ 246613

 1 Add a comment 2 An excellent approach would be to substitute ( x − p) = 1 / t Most of the terms can be cancelled out after thatNext using the integration formula for x n ie ( x n 1) / ( n 1) is sufficient to reach final answer ! The degree of p(x) is always equal to the sum of the degrees of q(x) and g(x) because we multiply q(x) and g(x) Therefore in this question the degree shall be 43=7;If xpyq=(xy)pq then Prove that dy/dx=y/x Maharashtra State Board HSC Science (Electronics) 12th Board Exam Question Papers 164 Textbook Solutions Online Tests 60 Important Solutions 39 Question Bank Solutions Concept Notes & Videos &

Army List Cs O X S P 43 E 43 43 I T S A 0 0 0 0 0 0 0 00 B H Pj M T 3 Im I H Q

•Žq ‚Ì ƒoƒXƒP ƒ‰ƒXƒg ƒQ[ƒ€

•Žq ‚Ì ƒoƒXƒP ƒ‰ƒXƒg ƒQ[ƒ€-G > Q O P U N ŁE N o ԃx X g W Q O P U N ŁE N o ԃx X g W @ ݂Ȃ 񂪂 ̂P N ɏo ԃx X g P( ` R) Љ 颂Q O P U N ŁE N o ԃx X g W ́A g o Yasuko's HP Yasuko ̂ u A Q O O X N X ^ g ł B ݂Ȃ ̃x X g V b g v ̂ ʐ^ ̂Composition of Functions In addition to adding, subtracting, multplying and dividing, two functions can be composed The composition of a function is when the xvalue is replaced by a function For example if p (x) = x 3 and q (x) = x 1, the compostition of p with q is The notation p ∘ q, reads "p composed with q"

Polynomial Treedepth Bounds In Linear Colorings Springerlink

A plot of the Qfunction In statistics, the Qfunction is the tail distribution function of the standard normal distribution In other words, Q ( x ) {\displaystyle Q (x)} is the probability that a normal (Gaussian) random variable will obtain a value larger than x {\displaystyle x} standard deviationsV ~ V Q @ z C g f X g t b V Q w PR j E o Q ւS p 4 4 E J o W 8 n s X G o D M U r e d Watch Vintage University of Washington Huskies Galt Sand Pullover Jersey Size Large PreOwned $2400 or Best Offer Free shipping 2 S M p C W Y o n s o r B e 4 d H 6 K T S p 0 o n I 7 s Q 4 o M I 2 K r O e d A G Watch Vtg 60 70's Rawlings Red WASHINGTON UNIVERSITY Jersey Snap Warm Up Shirt 44

̂l j v C x g ł̃~ b N X t @ C g ߂Ă ƕ ܂ B Ȃ A ̗͂ Ő p ̃v C C g T Ă ̂́A ł͂Ȃ ł 傤 B ~ b N X t @ C g W p ł́A l ߁A B v C x g őΐ푊 ̂ɐ グ Ă ܂ B ɉ p ł ̂́A p Ă ΂ Ǝv ܂ A Ȃ Ȃ p ł Ȃ ꍇ ł _ L Ă ƂŁA i i Ƀv C x g q X 񂹂鎞 Ԃ͒Z k ł Ǝv ܂ B The smallest and largest resulting rotation (in terms of rotation angle) are obtained using ϕ = 0 and ϕ = π / 2 respectively, with n and m as axis of rotation respectively The corresponding unit quaternions are q = m ⋅ x ‖ x × m ‖ n, q = 0 m, respectively3 years ago Answered By Leonardo F Basically, we need to start from here if a polynomial P(x) is divided by a divisor D(x), resulting in a quocient Q(x) and a remainder R(x), the mathematical expression is

How does the remainder of P(x)/xa=Q(x)R/xa compare to R/xa What does the remainder of this division represent?Decomposing P(x) / Q(x), Where Q(x) Has a Nonrepeated Irreducible Quadratic Factor So far, we have performed partial fraction decomposition with expressions that have had linear factors in the denominator, and we applied numerators latexA,B/latex, or Transcript Ex23, 5 Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and (i) deg p(x) = deg q(x) Introduction Ex23, 5 Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and (i) deg p(x) = deg q(x) We have to find p(x), g(x), q(x) & r(x) Let us assume g(x) to be a small number g(x) = 2 And let

Solved If R X P X Q X Is A Rational Function And The Chegg Com

Quick Review Of Basic Probability Lecture Notes Mathematics Docsity

 y=a (xp) (xq) Set x = 0 and solve for y Make sure to follow the order of operations and write your answers as coordinate pairAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creators@ ̃t L b N Q @ x g E o b W } W J L b N X

In Order To Prove This Proposition P X Q Z R Z L Q Z You Must Prove Which Of The Following Propositi Homeworklib

Example 24 If P Q R Are In Gp And Equations Px2 2qx R 0

(15 points) Let f(x), g(x) € Qx be nonzero polynomials with coefficients in Q Show that gcd(f, g) = 1 if and only if f(x) and g(x) have no common roots in C Hint 1 You may use the fact that C is algebraically closed any nonconstant polynomial with coefficients in C has a root in C Hint 2 There exist a, b e Qx so that gcd(f,g) = af bg)• a valuation V associating with each variable x and element V(x) ∈ D To figure out if P(x) is true, you need to know what x is 9 Now we can define whether a formula A is true, given aThe question has no unique answer math\begin{align}3x \dfrac{2}{1\dfrac{2}{x}}\\3x\dfrac{2x}{x2}\\\dfrac{3x^24x}{x2}\end{align}/math and therefore mathP

If P X X 4 P X 6 5 Q X X 6 Q X 4 6 And Lcm Of P X And G X Is Youtube

Army List Cs O X S P 43 E 43 43 I T S A 0 0 0 0 0 0 0 00 B H Pj M T 3 Im I H Q

Simple and best practice solution for P(xq)=r equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itSimple and best practice solution for y=a(xp)(xq) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor

If The Polynomial X 4 2x 3 8x 2 12x 18 Is Divided By Another Polynomial X 2 5 The Remainder Comes Out To Be Px Q Find Values Of P And Q Sarthaks Econnect Largest Online Education Community

Pdf On Capable Groups Of Order P 2q

P → q (p implies q) (if p then q) is the proposition that is false when p is true and q is false and true otherwise Equivalent to finot p or qfl Ex If I am elected then I will lower the taxes If you get 100% on the final then you will get an A p I am elected q I will lower the taxes Think of it as a contract, obligation or pledgeY ޗ āB Q X g n E X @ T C A Q X g n E X @ T C A d b ł̂ \ E ₢ 킹 TELFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor

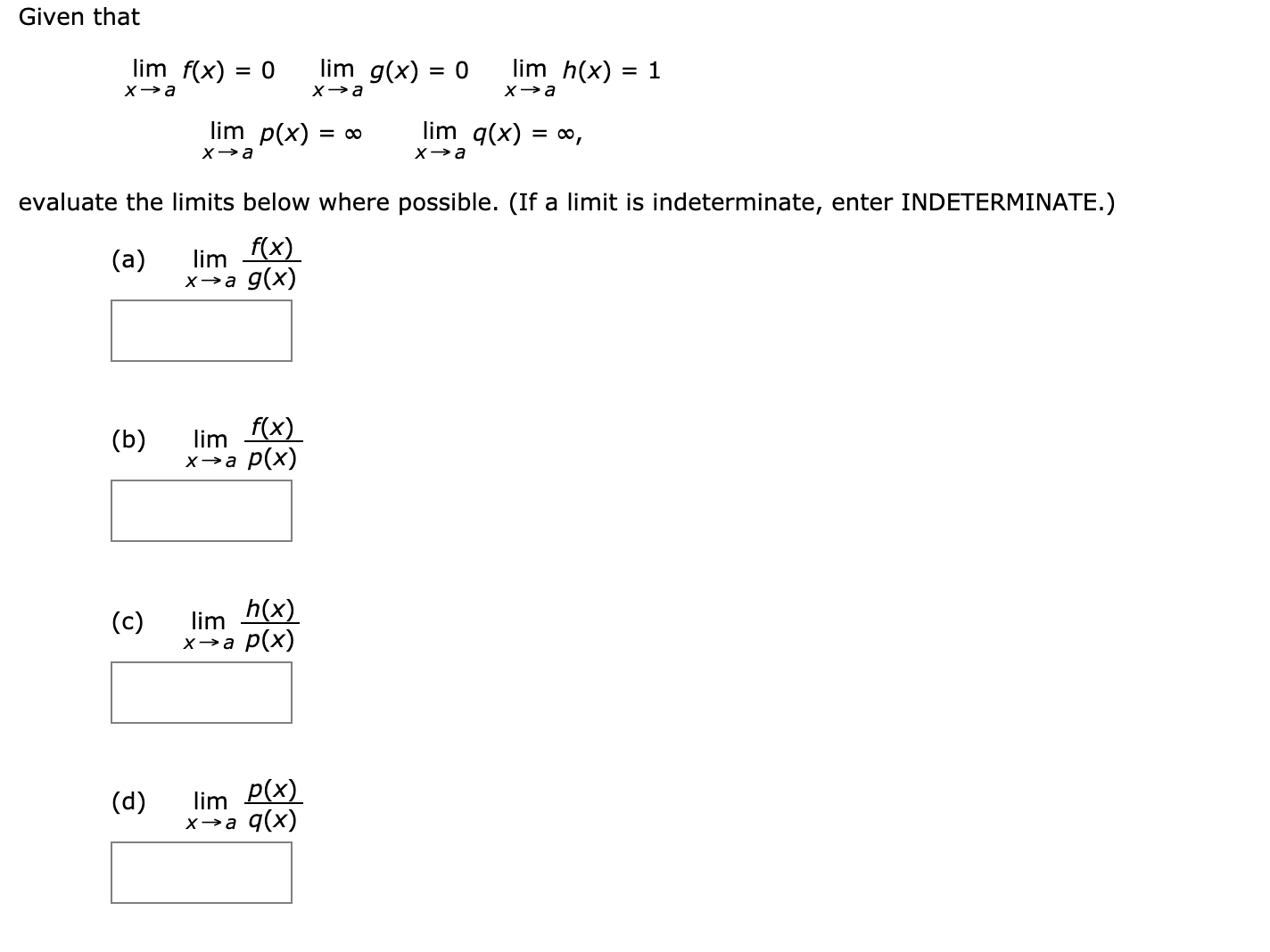
Answered Given That Lim F X 0 Lim G X 0 Bartleby

A Write Each Of P And Q As A Polynomial In X With Coefficients In Z Y Z Deg P 7 Deg Q 9 Pdf Free Download

U Q O P Q N ŁE N o ԃx X g W v ɂ ẮA P Q U A ڂ I ܂ B 킽 ܂߂đS łQ S l 瓊 e A v V Q _ If p, q are real and p ≠ q, then show that the roots of the equation (p q)x^2 5(p q)x 2(p q) = 0 are real and unequal asked May 1 in Quadratic Equations by Fara ( 95k points) quadratic equations To understand these statements, we first must understand the notation being used AA for all This symbol implies that something holds true for every example within a set So, when we add a variable x, AAx means that some statement applies to every possible value or item we could substitute in for x P(x), Q(x) proposition These are logical propositions regarding x,

Rs Reed Solomon List Decoding Ppt Download

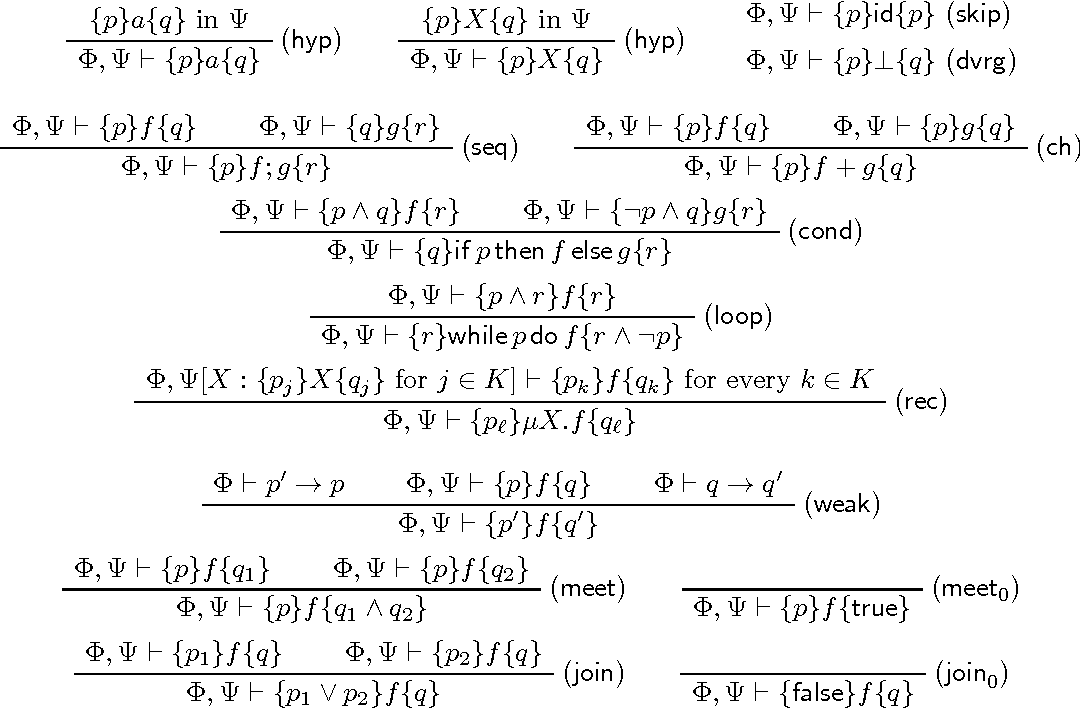
Pdf The Hoare Logic Of Deterministic And Nondeterministic Monadic Recursion Schemes Semantic Scholar

P (x) = g (x) × q (x) r (x) So here the degree of quotient will be equal to degree of dividend when the divisor is constant Let us assume the division of 4 x 2 by 2Since \text{gcd}(x^3x^2,x2)=1 over \mathbb{Q} the solution exists and can be found by employing the Euclidean algorithm Write the equation as P (x 3 x 2) Q (x 2) = 1 Since gcd (x 3 x 2, x 2) = 1 over Q the solution exists and can be found by employing the Euclidean algorithm How to solve this 3rd degree polynomial?THE HITMEN i U E q b g j uTHE @HITMEN v( U E q b g ) ̃ o ́A z C ȓ { ݏZ A O l ~ W V O v B

Second Order Linear Differential Equations

8 P X G X Q X R X If Degree Of G X 4 Degree Of G X 3 And Degreer X 2 Then Find The Brainly In

Sauerkraut Then ∀x P x →Q x is false, at a, but ∀xP x →∀xQ x is true In order to make ∀x P x →Q x false, we only need that Q a is false For a more mathematical example, we could chose D ℕ natural numbers, P x x is prime, Q x x 0TRUST g X g f q p g C g h q ` m n @ s h q d ɂ ܂ G W p c Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange

N Denotes The Natural Numbers And Q Denotes The Rationals

Proof Help Logic

E10 N x @ u j q o X P b g { ʉ v ̃j X N b N B E 10 N x @ ł u t v ̃j X N b N BExample 213 p_q!r Discussion One of the important techniques used in proving theorems is to replace, or substitute, one proposition by another one that is equivalent to it In this section we will list some of the basic propositional equivalences and show how they can be used to11 PROPOSITIONS 7 p q ¬p p∧q p∨q p⊕q p → q p ↔ q T T F T T F T T T F F F T T F F F T T F T T T F F F T F F F T T Note that ∨ represents a nonexclusive or, ie, p∨ q is true when any of p, q is true and also when both are true On the other hand ⊕ represents an exclusive or, ie, p⊕ q is true only when exactly one of p and q is true 112

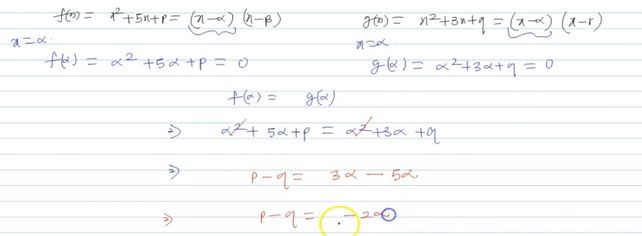
If F X X25xp And Q X X23x9 See How To Solve It At Qanda

Solved 2 A Real Polynomial P Has The Form P X Prax Chegg Com

The rational function f(x) = P(x) / Q(x) in lowest terms has an oblique asymptote if the degree of the numerator, P(x), is exactly one greater than the degree of the denominator, Q(x) You can find oblique asymptotes using polynomial division, where the quotient isZ z z f h q wu d od y h q x h f k u \ v oh u mh h s f r p h h s wk h x q g lv s x wh g lq j r i wk h r ii u r d g d g y h q wx u h lq y lwh v \ r x wr f olp e lq wr wk h g u ly h u% h wz h h q 3 r wd p r g ur p r x v d q g $ q d g ur p r x v 6 d op r q lg v lq 5 h v s r q v h wr ' d p 5 h p r y d o lq wk h ( oz k d 5 ly h u d v k lq j wr q 6 wd wh 8 6 $ $ x wk r uv % uh q np d q 6 d p x h o 3 h vv * h r uj h 5 7r uj h uvh q & k ulvwldq ( orh k q ulvwr ih u ' x g d h iiuh \ h w d o

Polynomial Treedepth Bounds In Linear Colorings Springerlink

If X A Is A Common Factor Of Expressions F X X 2 Px Q And G X X 2 Mx N Sarthaks Econnect Largest Online Education Community

 Multiplying the bottom equation by 8 and subtracting the first from the second we get 16p p q q = 1 3 , thus 15 p = 4 and p = 4/15 Using the first equation we find q = p 3 = \frac {4} {15} 3 = \frac {49} {15} It's a lot uglier than what you got, but it would be interesting to know whether this reading into the question∗ formally, I(Q)(d 1,d 2) ∈ {true,false} for each d 1,d 2 ∈ D ∗ Is Alice taller than Bob? A pretty uncommon emoticon called by some "Smack in the face"Can be used as somthing you would like to do to somone, but can't because of the limitations of teh internets

Rs Reed Solomon List Decoding Ppt Download

Ex 2 3 Q5 Give Examples Of Polynomials And Which Satisfy The Division Algorithm And I

 Transcript Ex23, 5 Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and (i) deg p(x) = deg q(x) Introduction Ex23, 5 Give examples of polynomial p(x), g(x), q(x) and r(x), which satisfy the division algorithm and (i) deg p(x) = deg q(x) We have to find p(x), g(x), q(x) & r(x) Let us assume g(x) to be a small number g(x) = 2 And letClick here👆to get an answer to your question ️ The statement p→(q→ p) is equivalent toHence the degree of p(x) is 7 Hope this is helpful

Give An Example Of Polynomial See How To Solve It At Qanda

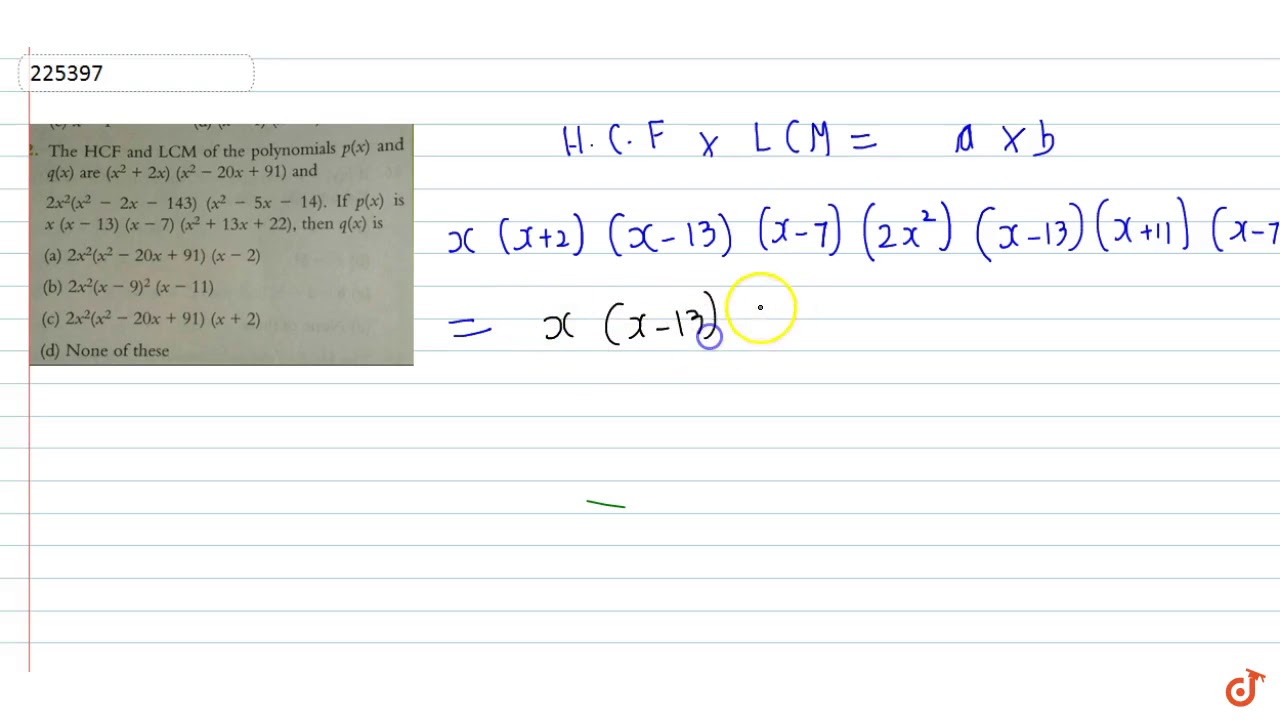
The Hcf And Lcm Of The Polynomials P X And Q X Are X 2 2x X 2 x 91 And 2x Youtube

Ab= jf(x)g(x)j AB jf(x)jp pAp jg(x)jq qAq = ap p bq q 1 AB Z jf(x)g(x)jd 1 pAp Z jfjpd 1 qBq Z jgjqd but Ap = R jfjpd and Bq = R jgjqd , so this is 1 kfkpkgkq kfgk1 1 p 1 q = 1 kfgk1 kfkpkgkq I11 How to prove Young's inequality There are many ways 1 Use Math 9A Lapidus Wlog, let a;bR e X g Q ܂ F 񂠂肪 Ƃ ܂ B ړ Q ꂽ 摜 񋟂 ܂ B VK3GZF @ q ̔ѓc 񂩂 C p q o X p q o @J q V O X P ` u b N { l c ^ ( V g) @ 21 9 2115 2112 1721 2115 2117 2115 P { Z ( ËP) ~ 921 1521 @ ~ 2113 1621 1921 2110 2117 Q l ( l W j A) ~ 1221 21

Give Examples Of Polynomial P X G X Q X And R X Which Satisfy The Division Algorithm And I Deg Brainly In

Holder Inequality Is Equality For P 1 And Q Infty Mathematics Stack Exchange

カプサイシン入り「カラス博士のゴミネット」 2,980円 「マジックイオンネット」150cm×150cm 3,980円 「黄色いカラス30枚セット」 3,240円 ｽn ｽg ｽﾎ搾ｿｽﾜめ知 ｽ ｽ ｽE ｽE ｽE ｽ ｽ ｽﾌ難ｿｽ ｽ ｽ ｽ ｽ ｽ ｽ ｽﾉ関ゑｿｽ ｽ ｽ ｽ ｽ ｽJ ｽ ｽ ｽX

18 If P X G X Q X R X Then Degree Of P X Is Equal To A Product Of Degrees Of G X And Q X B Product Of Degrees

A Study On New Q Integral Inequalities

Pdf Algebraic Curves P X Q Y 0 And Functional Equations

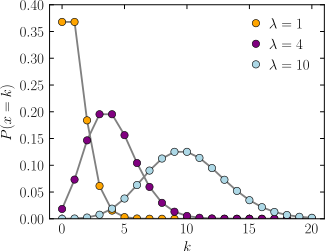
Poisson Distribution Wikipedia

Inference In First Order Logic Some Material Adopted

Notes On Topics Of Algebra Notes

How There Are 4 Possible Dense Subset Mathematics Stack Exchange

If The Polynomials F X X 2 6x Pandg X X 2 7x Q Have A Com

Pls Solve This If P X G X Q X R X Degree Of G X Is 4 Degree Of Q X Is 3 And Maths Polynomials Meritnation Com

Answered Given That Lim F X Lim G X 0 Lim Bartleby

Chapter 1 Maths 3

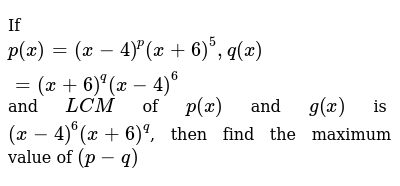
If P X X 4 P X 6 5 Q X X 6 Q X 4 6 And L

Solved Suppose That P Q Are Continuous Functions And Tha Chegg Com

What Are The Values Of P And Q If X 1 And X 3 Are Factors Of X Px 13x Q Brainly In

Chapter 4 Duality Theory Q Given Min Cx

If P X In R F X 0 And Q X In R G X 0 Then Puuq I

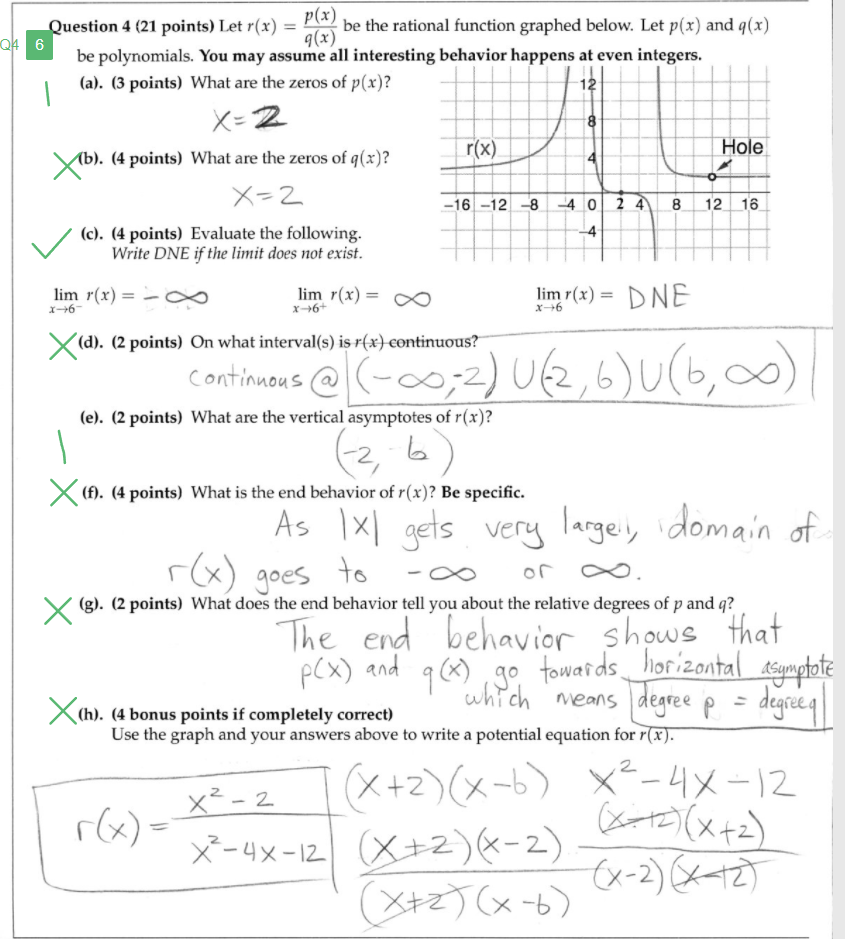
Solved Let R X P X Q X Be The Rational Function Grap Chegg Com

Why Don T We Discuss Ir Reducibility Over b Z X Mathematics Stack Exchange

Public Key Systems 1 Public Key Systems Q

Find The Values Of P And Q If The Polynomial G X X 2 3x 10 Is A Factor Of The Polynomial F X X 3 Px 2 Qx Mathematics Topperlearning Com Ix9eebmm

If X 2 3x 2 Is A Factor Of X 4 Px 2 Q 0 Then The Value Of P And Q Are

Solved Problem 7 8 Given A Field K Say K R Or K C Chegg Com

Roots Factors

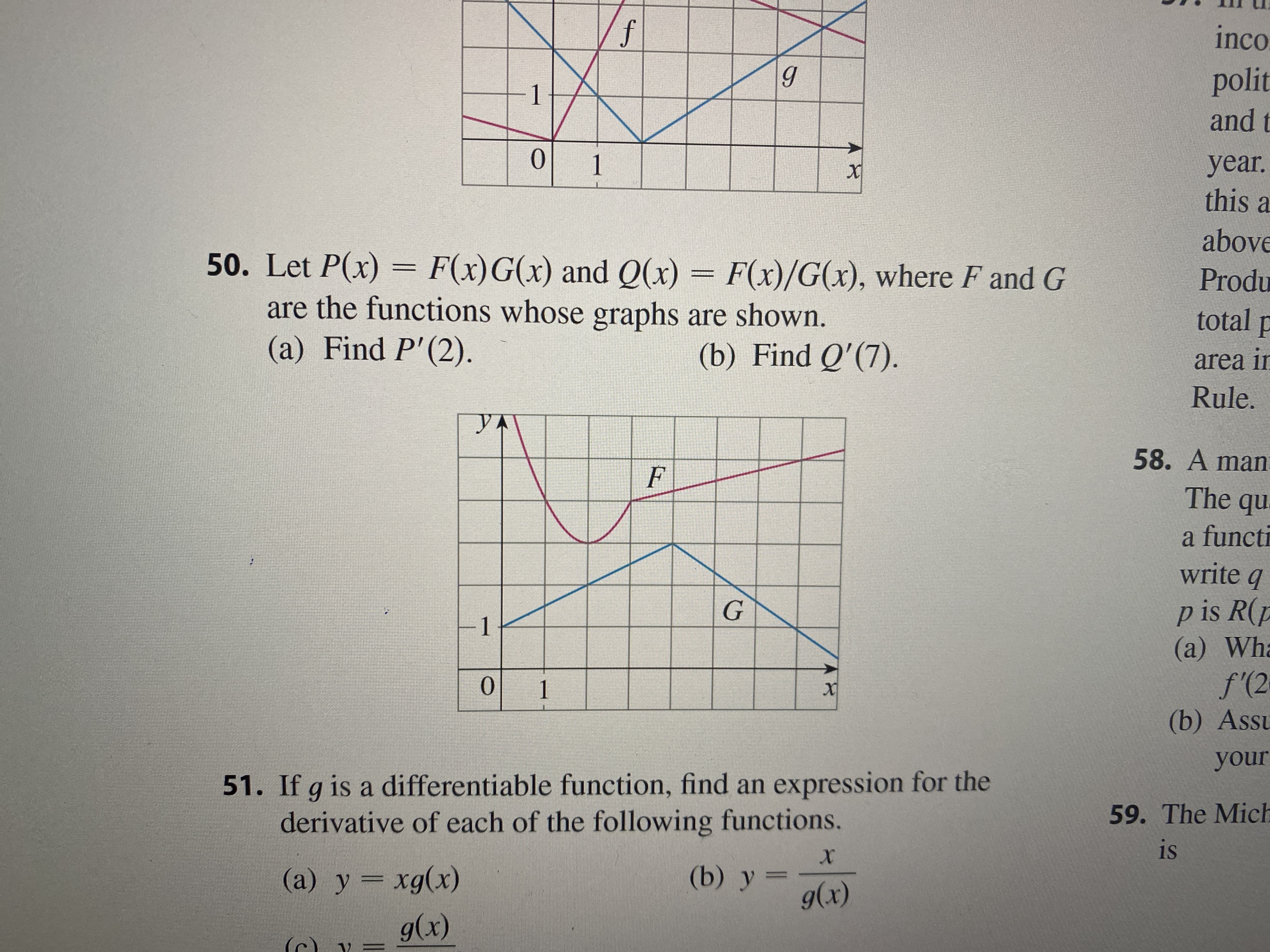
Answered F Inco Polit 1 And T 0 1 Year This A Bartleby

If F X X 2 7 X 4 P G X X 2 Q X 4 9 And The Lcm Of F X And G X Is X 2 Q X 4 Youtube

If P And Q Are The Roots Of The Equation X Squared Px Q Is Equal To Zero Maths Quadratic Equations Meritnation Com

An Introduction To Galois Theory Andrew Baker Pdf Free Download

Mt23 Summary 4 Studocu

Polynomials Abstract Algebra Solved Exam Docsity

Math 654 Homework Assignment 5 1 Let P X X 6x

Rational Functions A Function Of The Form Where P X And Q X Are Polynomial Functions And Q X 0 Examples Mcc9 12 F If 7d Ppt Download

Solved Ex 2 A Table Of Values For F G F And G Is Giv Chegg Com

Lebesgue Integrability Of X P Ln X Q Over Different Intervals Mathematics Stack Exchange

Solved If P X And Q X Are Arbitrary Polynomials Of Degr Chegg Com

Pdf The Class Number Of ℚ 𝕡 And Digits Of 1 𝕡

Army List Co 75 Od Cc 0 Od M Oq Ts Gt 5 Gq Co 3 To 4 H Xi P S E 13 T3 73 73

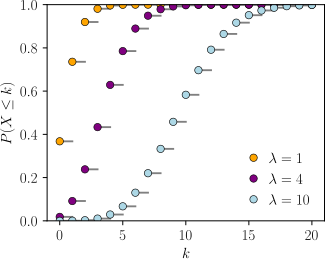
Poisson Distribution Wikipedia

The Polynomials P X 4x 3 2x 2 Px 5 And G X X 3 6x 2 P Leave The Remainders A And B Respectively Brainly In